2023년 3월 23일 치러진 3월 학력평가 수학 3점 문제 풀이입니다. 사실 정답을 위한 풀이보다는 문제를 1.보고 2.어떤 생각을 거쳐 3어떻게 답을 도출하는 접근을 해야 하는지를 중점으로 알려드리려고 합니다.
점수를 높이고 싶은 학생 뿐만 아니라 안정적인 1, 2등급을 유지하고 싶은 학생들에게도 3점 정복은 필수적인 과제입니다.
그럼 제 노하우를 녹인 풀이를 보시고 올바른 수학 모의고사 공부법을 통해 3점 문제 정복을 하시기 바랍니다!
공통 과목 5지선다형
3번

등비수열 문제의 경우 보통 첫항과 공비를 미지수로 놓고 풀이를 시작합니다. 연립방정식을 풀 때 미지수가 n개가 있다면 그 미지수들에 관한 서로 다른 방정식(혹은 어떤 형식의 조건)이 최소 n개 필요하다는 뜻입니다.
즉, 첫 항을 미지수 a, 공비를 r 이라고 두면(이때, r은 0이 아님) 미지수를 2개 잡았기 때문에 방정식이 2개 필요하다는 뜻이고, 공교롭게도 주어진 식이 2개입니다.
그럼 첫 번째 식은 \( a_5 = ar^4 = 4 \)
두 번째 식은 \( a_7 = ar^6 \), \( 4a_6 -16 = 4ar^5 -16 \) 에서 \( ar^6=4ar^5 -16 \) 입니다
이 두 식을 연립해서 풀면 \( a= {1 \over 2} , r=2 \)가 나와 \( a_8= ar^7 = 32\)임을 알 수 있습니다.
<답 1번>
4번

이 문제를 보는 순간 a를 구하는 것을 우선으로 생각해야 하고, 이때 정적분 하는 범위가 0이면 적분값도 0이라는 정적분의 성질이 활용됩니다.
즉 \( \int _{ 1} ^{x } {f(t) }dt = x^3 -ax +1 \) 에서 x 에 1을 넣으면(모든 실수 x에 대하여 만족시키는 식이니 어떤 실수든 넣어도 됩니다) 좌변의 값이 0이니 우변의 값도 0이고, 1-a+1=0 에서 a의 값은 2로 정해지게 됩니다.
문제에서 물어본 f(2)를 구하기 위해서는 f(x)의 식을 알아야 하고, \( \int _{ 1} ^{x } {f(t) }dt = x^3 -2x +1 \) 이 식은 모든 실수에 대한 항등식이니 양 변에 대해 미분을 해도 무방합니다. 미분하면 \( f(x)=3x^2 -2 \)이고, 따라서 f(2)의 값은 10입니다.
<답 2번>
5번
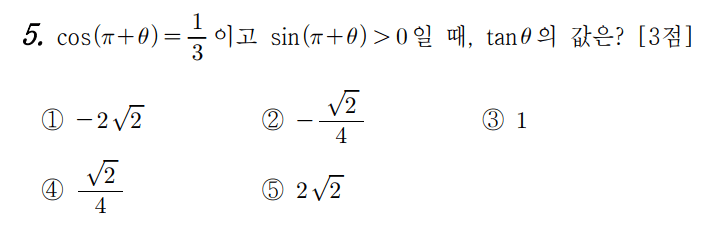
간단한 삼각함수 문제입니다.
\( cos(\pi + \theta) = -cos \theta \) 임을 이용해 \( -cos \theta = – {1 \over 3} \) 을 알고
\( sin(\pi + \theta) = -sin \theta > 0 \) 에서 \( sin \theta < 0 \) 이므로 sin과 cos이 모두 음수인 \( \theta \) 는 제3사분면의 각임을 알 수 있습니다
\( -cos \theta = – {1 \over 3} \)이고, \( sin \theta < 0 \) \( sin^2 \theta + cos^2 \theta = 1 \) 이라는 삼각함수의 성질을 이용하면 \( sin \theta = – {2\sqrt2 \over 3} \) 이고, \(tan \theta = {sin \theta \over cos \theta} = 2 \sqrt 2\) 임을 알 수 있습니다
<답 5번>
6번

함수의 연속 관련 문제입니다. 이런 유형의 문제는 불연속의 가능성이 있는 지점만 연속인지 확인하면 됩니다.
\( f(x) \) 함수 자체는 \( x <2 \) 라는 부분만 보면 연속, 마찬가지로 \( x \geq 2\) 인 범위에서만 보면 각각 연속입니다. 즉 불연속의 가능성이 있는 부분은 x가 2 언저리에 있을 때입니다.
+++
여기서 잠깐 함수의 연속의 정의를 알고 넘어가면 좋습니다.
함수 f(x) 에서 x=a 에서 함숫값과 극한값이 모두 존재하고 그 값이 같을 때 x=a 에서 연속이라고 한다.
이를 식으로 나타내면 \( \lim \limits_{x \rightarrow a} f(x) = f(a) \)
- f(x)가 x=a 에서 정의되어 있어야 하고(즉, f(a)라는 값이 존재해야 함)
- 그리고 \( \lim \limits_{x \rightarrow a} f(x) \) 가 존재하는데
- 하필 1. 2.의 두 값이 같은 상태, 즉 \( \lim \limits_{x \rightarrow a} f(x) = f(a) \)이면 연속인 겁니다.
그리고 2번의 “그리고 \( \lim \limits_{x \rightarrow a} f(x) \) 가 존재하는데” 라는 말은 f(x)의 x=a에서의 좌극한값과 우극한값이 같으면 되는 겁니다(참고로 극한값이 존재한다는 말은 함숫값이랑은 상관이 없습니다. 그냥 좌,우극한값만 서로 같으면 됩니다. 만약에 극한값이 함숫값과 같다면 그것이 ‘연속’을 의미합니다)
결국 연속 여부 문제에서 확인할 것은 \( \lim \limits_{x \rightarrow a+} f(x) = \lim \limits_{x \rightarrow a-} f(x) = f(a) \) 이라는 것만 확인하면 됩니다(우극한=좌극한=함숫값)
간단한 문제에서 설명이 길어졌는데, 무엇이든 정의를 정확히 알고 가면 좋습니다…ㅎ 그래야 문제를 풀 때 어떤 기준으로 문제를 풀 지 헷갈리지 않을 수 있습니다.
다시 풀이로 돌아와서, 결국 f(x)는 x=2 언저리에서 불연속의 가능성이 있으므로, \( \{f(x)\}^2 \) 또한 x=2 언저리에서만 불연속의 가능성이 있습니다. 그럼 우리는
\( \lim \limits_{x \rightarrow 2+} \{f(x)\}^2= \lim \limits_{x \rightarrow 2-}\{f(x)\}^2 = \{f(2)\}^2\) 임을 확인하면 됩니다.
이 식을 정리하면 \( (5-2a)^2 =1 \)이라는 식을 얻게 되고, 따라서 a=2 or a=3 이라는 값을 얻게 되어 가능한 상수 a의 값의 합은 5가 됩니다(혹은 \( (5-2a)^2 =1 \) 이 이차방정식의 근과 계수의 관계를 써도 되긴 합니다)
<답 1번>
7번
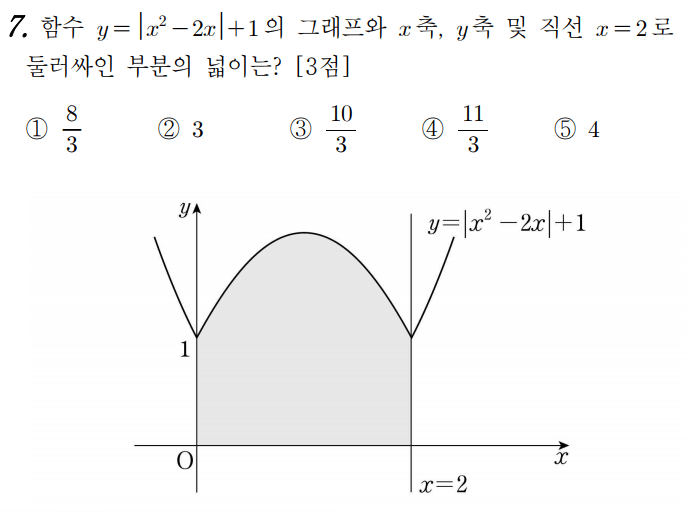
그래프가 그려져 있기 때문에 직관적으로 판단하기 쉬운 문제입니다(아마 그래서 3점..? 4점이었으면 절댓값 기호로 인해 꺾이는 부분이 포함되었을 듯)
절댓값 내부의 식 \(x^2 -2x \)는 \( 0 \leq x <2 \) 에서는 0 이하이고(즉, \(-x^2 +2x \) )
\( (x \geq 2, x < 0 ) \)에서는 0 이상입니다(즉, \(x^2 -2x \) 그대로)
우리가 구할 부분의 넓이는 \( \int _{ 0} ^{2 } ( \vert{x^2 -2x }\vert +1 ) dx \) 인데, 정적분의 범위가 0에서 2 까지임을 고려하면 \( \vert{x^2 -2x }\vert \)는 \(-x^2 +2x \) 로 생각하면 됩니다.
\( \int _{ 0} ^{2 } ( \vert{x^2 -2x }\vert +1 ) dx = \int _{ 0} ^{2 } ( -x^2 +2x +1 ) dx \) 이고, 이를 계산하면 답은 \( 10 \over 3\) 입니다.
<답 3번>
8번

내분점을 구하는 식을 알고 있는지 물어보는 문제입니다. 내분점 식만 알고 있다면 미지수가 m 하나이기 때문에 그냥 방정식 푸는 문제입니다.
내,외분점 공식을 알려드리면
A(a), B(b) 를 m:n 으로 내,외분한다고 했을 때 (m,n>0)
내분점 : \( {mb + na} \over {m+n} \)
외분점 : \( {mb – na} \over {m-n} \)
다시 문제로 돌아와서 \( \overline {AB} \) 를 2:1 로 내분하면
\(( {{2(m+3) + 1(m)} \over {2+1}} ,{ {2(m-3) + 1(m+3)} \over {2+1}} )\) , 즉 \( (m+2,m-1) \) 이고, 이 점이\( y=log_4 (x+8) +m-3 \) 위에 있으므로 \( (m+2,m-1) \)를 대입해서 방정식을 풀어주면 됩니다.
계산하면 m=6이 답입니다
<답 5번>
공통 과목 단답형
16번

로그의 기본 성질을 이용하는 문제입니다. 결국 이런 로그 계산 문제는 밑을 통일시켜서 계산해줘야 하기 때문에, 밑을 어떻게 통일시킬지를 중점적으로 생각해 봅니다.
\( log_2 96 \) 의 밑과 \( log_6 {2} \) 의 진수가 2로 같음에 집중해 봅시다. 로그의 역수의 경우 밑과 진수를 바꿀 수 있습니다
기억해 두기!
\( log_a b = {{1} \over {log_b a}} \)
단, a, b는 양수이고 1이 아님
그러므로 \( {{1} \over {log_6 2}} = log_2 6 \)이고, 따라서 \( log_2 96 – {{1} \over {log_6 2}} =log_2 96 – log_2 6 = log_2 {96\over6} = log_2 16=4\) 입니다
17번

접선 문제입니다.
접선 문제 유형은 세 가지 정도로 나뉘는데,
- 접점이 주어져 있을 때
- 함수 밖의 점에서 접선을 그을 때
- 기울기가 주어져 있을 때
입니다. 접점이 주어져 있으면 그냥 원 함수를 미분해서 접점의 x좌표를 넣으면 접선의 기울기가 나올 테고, 그 이후는 쉽습니다.
함수 밖의 점이나 기울기가 주어져 있을 경우, 접점을 \((t,f(t))\) 등으로 임의로 잡아 문제를 풀어나가면 됩니다. 결국은 모든 경우에 접점을 구해야 하는데, 접점이 주어져 있을 때는 굳이 구할 필요가 없을 뿐입니다.
이 경우는 접선의 기울기가 4로 주어져 있기 때문에, 접선을 임의로 설정하고 문제를 풀어 나가면 됩니다.
접점을 \( (t, 2t^4 -4t +k) \) 로 둘 수 있고, 곡선을 미분하면 \( y’=8x^3 -4\)가 나오기 때문에 접점에서의 접선의 기울기는 \( 8t^3 -4\) 이라고 할 수 있습니다.
접선의 기울기가 4였기 때문에 \( 8t^3 -4=4\)에서 \( t=1 \)이고, 따라서 접점의 좌표는 \( (1, 2-4+k) =(1,k-2) \) 이며, 이 점은 접점이기 때문에 접선 위의 점이고, \(y=4x+5 \) 접선의 방정식에 대입하면 k는 11이 나옵니다
<답 11>
18번

방법은 여러 가지 있는데 서로 크게 다르지 않습니다. 저의 경우 \( (1-\alpha_n )(1-\beta_n )\) 이라는 식을 보자마자 \( 1-(\alpha_n + \beta_n ) + \alpha_n \beta_n \) 이 전개식을 떠올리고 근과 계수의 관계를 이용하려고 했습니다.
근과 계수의 관계에 의해 \( \alpha_n + \beta_n = 5n \), \( \alpha_n \beta_n = 4n^2 \)이므로 \( (1-\alpha_n )(1-\beta_n ) = 1-(\alpha_n + \beta_n ) + \alpha_n \beta_n = 1-5n+4n^2 \) 이고, 따라서 구하는 식은 \( \sum \limits_{n=1}^7 {1-5n+4n^2} \) 이고, 따라서 \( \sum \limits_{n=1}^7 {1} -5 \sum \limits_{n=1}^7 {n} + 4 \sum \limits_{n=1}^7 {n^2} \) 을 계산하면 427이 나옵니다.
참고로
- \( \sum \limits_{n=1}^k {n} = {{k(k+1)} \over 2} \)
- \( \sum \limits_{n=1}^k {n^2} = {{k(k+1)(2k+1)} \over 6} \)
- \( \sum \limits_{n=1}^k {n^3} = ({{k(k+1)} \over 2})^2 \)
임은 외우고 있어야 합니다.
<답 427>

위치를 미분하면 속도, 속도를 미분하면 가속도 / 가속도를 적분하면 속도, 속도를 적분하면 위치
이 개념을 머리 속에 넣고 있어야 합니다. 위치가 변화하는 정도가 빠르기, 즉 속도이니까 위치의 순간변화율, 즉 미분값이 그 순간의 속도라고 생각하면 편합니다.
\( v_1 (t), v_2 (t) \) 를 적분한 것, 즉 두 점 P, Q의 위치를 \( x_1 (t), x_2 (t) \) 라고 하면 \( x_1 (t)=t^3 -{ 15t^2 \over 2} +kt + c_1 \), \( x_2 (t)=-t^3 -{ 9t^2 \over2} + c_2 \) 입니다. \( c_1, c_2 \)를 빼먹는 경우가 있는데, 절대 안 빼먹도록 습관을 들어줘야 합니다.
보통 문제들이 원점에서 출발이라서 t=0 일 때 위치도 0 이기 때문에 \( c_1, c_2 =0 \)여서 큰 문제가 없었던 것이지, 출발 당시의 위치가 서로 다른 문제도 나올 수 있기 때문에 주의하셔야 합니다.
점 P, Q가 한 번만 만난다는 것은 위치 \( x_1 (t), x_2 (t) \) 의 차이가 0인 순간이 ‘t가 0초 이후에‘ 한 번만 존재한다는 뜻입니다. t가 음수인 것은 우리가 신경을 써서 없다고 봐 줘야 합니다!
\( x_1 (t)- x_2 (t) = t(2t^2 -12t+k)=0 \) 이 방정식의 ‘양의’ 근이 1개여야 하므로 \( 2t^2 -12t+k=0 \) 이 중근을 가져야 합니다. 이때! 사실 양근 하나와 0 이하의 근 하나, 총 두 개의 근을 가져도 됩니다! 이런 것을 놓치면 안 되는데, 문제에서 k가 양수라고 했기 때문에 양근 하나와 0 이하의 근 하나를 가질 수 없어 중근을 가져야만 하는 것입니다.
계산은 판별식을 쓰면 \( {D \over 4} = (-6)^2 -2k =0 \) 에서 k 값은 18입니다.
<답 18>
마치면서
처음에 말했듯이 수학 3점 문제는 상,중,하위권을 가릴 것 없이 중요합니다. 물론 모의고사마다 답지를 구할 수 있지만 제가 시간을 써서 해설을 하는 이유는 문제를 보고 나서의 사고 과정을 알려드리기 위함입니다.
‘문제의 어떤 포인트를 보고 어떻게 생각을 시작해야 하는지’를 알려드리는 것이 목적이니 단순이 해설 확인보다는 제 사고 과정을 참고하시면 좋겠습니다.
그리고 아무래도 글로 쓰다 보니 제가 말하고 싶은 바를 다 담지 못하는 부분도 있습니다(수식 쓰기가 꽤 힘든 작업이네요…ㅎ). 나중에 시간을 내서 영상을 만들거나 할 수도 있으니 관심 많이 가져주세요!
다들 화이팅이요~~~
